Fórmula de Bháskara

Pi

"π é o número que representa a quociente entre o perímetro de uma circunferência e o seu diâmetro; por outras palavras, se uma circunferência tem perímetro p e diâmetro d, então aquele número é igual a p/ d. É representado pela letra grega π. A letra grega π (lê-se: PI), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde."

Curiosidade

Escolha uma sequência de algarismos, um número que lhe seja familiar (número de telefone, o número do seu bilhete de identidade…).

Experimente procurar a sequência que escolheu no número, para tal consulte a página:

http://www.atractor.pt/fromPI/PIsearch.html

A procura é feita pelo computador nos primeiros 2 147 483 000 algarismos do Pi e, aí, existe uma forte probabilidade de encontrar o número que escolheu, se este não tiver mais que nove algarismos.

Matemática em clima de Natal!!!!

Que situação chegamos, isto é vergonhoso!

Ensino de matemática em 1950

Um cortador de lenha vende um carro de lenha por R$ 100,00. Sabendo que o custo de produção desse carro de lenha é igual a 4/5 do preço de venda, calcule o lucro.

Ensino de matemática em 1970

Um cortador de lenha vende um carro de lenha por R$ 100,00. O custo de produção desse carro de lenha é igual a 4/5 do preço de venda ou R$ 80,00. Qual é o lucro?

Ensino de matemática em 1980

Um cortador de lenha vende um carro de lenha por R$ 100,00. O custo de produção desse carro de lenha é R$ 80,00. Qual é o lucro?

Ensino de matemática em 1990

Um cortador de lenha vende um carro de lenha por R$ 100,00. O custo de produção desse carro de lenha é R$ 80,00. Escolha a única resposta certa que indica o lucro:
( ) R$ 20,00
( ) R$ 40,00
( ) R$ 60,00
( ) R$ 80,00
( ) R$ 100,00

Ensino de matemática em 2000

Um cortador de lenha vende um carro de lenha por R$ 100,00. O custo de produção desse carro de lenha é R$ 80,00. O lucro é de R$ 20,00. Está certo?
( ) SIM
( ) NÃO

Ensino de matemática em 2010

Um cortador de lenha vende um carro de lenha por R$100,00. O lucro é de R$20,00. Se você souber ler, coloque um X ao lado do R$20,00.
( ) R$ 20,00
( ) R$ 40,00
( ) R$ 60,00
( ) R$ 80,00
( ) R$ 100,00

Gostei muito deste Relogio, é minha cara.

Teoria Da Probabilidade

View more documents from mascena

Pra Não perder o humor!!! kkkkkk

Jogos: Tangram

Cruzadinha com Números.

ESCOLA ESTADUAL CARLOS IRIGARAY FILHO

Professores: Fabio Jr. Paes & Mileide Tonsis.

Alunos participantes:1º Ano do 2º segmento EJA. Ens. Fundamental. Noturno. 6º ano, matutino.

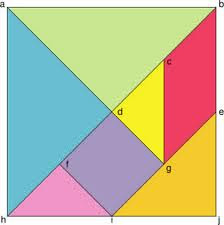
Tema: TANGRAM.

Natureza prioritária – Matemática.

JUSTIFICATIVA ( Projeto em desenvolvimento)

O tangram é uma arte chinesa que permite estudarmos as formas geométricas, a partir do quadrado, onde as figuras formadas tem, áreas e perímetros diferentes. É uma atividade lúdica onde podemos explorar inúmeras possibilidades alem da matemática, arte e historia desta arte – matemática.

TANGRAM E SUA HISTÓRIA

O Tangram é um quebra-cabeça chinês formado por 7 peças (5 triângulos, 1 quadrado e 1 paralelogramo) Com essas peças podemos formar várias figuras, utilizando todas elas sem sobrepô-las. Segundo a Enciclopédia do Tangram é possível montar mais de 1700 figuras com as 7 peças. Esse quebra-cabeça, também conhecido como jogo das sete peças, é utilizado pelos professores de matemática como instrumento facilitador da compreensão das formas geométricas. Além de facilitar o estudo da geometria, ele desenvolve a criatividade e o raciocínio lógico, que também são fundamentais para o estudo da matemática. Não se sabe ao certo como surgiu o Tangram, apesar de haver várias lendas sobre sua origem. Uma diz que uma pedra preciosa se desfez em sete pedaços, e com elas era possível formar várias formas, tais como animais , plantas e pessoas. Outra diz que um imperador deixou um espelho quadrado cair, e este se desfez em 7 pedaços que poderiam ser usados para formar várias figuras. Segundo alguns, o nome Tangram vem da palavra inglesa "trangam", de significado "puzzle" ou "buginganga". Outros dizem que a palavra vem da dinastia chinesa Tang, ou até do barco cantonês "Tanka", onde mulheres entretiam os marinheiros americanos. Na Ásia o jogo é chamado de "Sete placas da Sabedoria".

METODOLOGIA

i – Apresentação teórica do Tangram.

ii – Apresentação de jogos on line com Tangram. LIED.

iii – Produção de tangrans em EVA e isopor.

iv – Produção de textos enigmáticos.

v – Produção Estudo de área e perímetro das figuras.

vi – Estudo de figuras geométricas.

vii – Produção de mini-tangrans (lembrança para a Mostra Cultural).

viii – Produção de tangrans em isopor em forma de escultura para decorar o ambiente na Mostra Cultural.

ix – Apresentação e exposição dos resultados na Mostra Cultural.

ESTABELECIMENTOS DE OBJETIVOS

* Criar e reproduzir figuras.

* Mostrar que a Matemática pode ser divertida;

* Familiarizar o aluno com as figuras básicas da Geometria;

* Desenvolver o raciocínio lógico para a resolução de problemas, coordenação motora e habilidades na utilização dos materiais a serem utilizados;

* Estimular a participação do aluno em atividades conjuntas para desenvolver a capacidade de ouvir e respeitar a criatividade dos colegas, promovendo o intercâmbio de idéias como fonte de aprendizagem para um mesmo fim.

CRONOGRAMA

ATIVIDADES	AGOSTO	SETEMBRO	OUTUBRO	NOVEMBRO
Leituras / teorias.	X
Construção dos tangrans	X	X	X
Apresentação/ Feira de Ciências				X

PLANILHA DE GASTOS

DESCRIÇÃO/ QUANTIDADE	VALOR R$	PREVISÃO/ DATA	T O T A L
EVA – varias cores.
Isopor . 5cm.
Cola branca.
Tesouras.
Papel.
Tinta guache.(azul, amarelo, vermelho, verde).
Estilete.
Cola quente.
Palitos de espetinho.
Imã
Bases de maderite MDF. 40x40.

REFERÊNCIAS BIBLIOGRÁFICAS

http://www.alunosonline.com.br/matematica/tangram.html

http://pt.wikipedia.org/wiki/Tangram

http://rachacuca.com.br/jogos/tangram

lúdica

http://www.klickeducacao.com.br/conteudo/pagina/0,6313,POR-1929-16168-,00.html

LEITURAS AO VENTO: Projetode incentivo à leitura, destinado a criança...

LEITURAS AO VENTO: Projetode incentivo à leitura, destinado a criança...: Projeto de incentivo à leitura, destinado a crianças e jovens, realizado todos os domingos das 15h às 18h na praça da Catedral de Maring...

http://lh6.ggpht.com/_tSgZoxiuQ-4/SxaFn2dEadI/AAAAAAAAANw/_wgergwkxhw/s400/601.png

Equação do AMOR

Alguns pensamentos de Pitágoras:

Filósofo e matemático Grego

· Não é livre quem não consegue ter domínio sobre si.
· Todas as coisas são números.
· Aquele que fala semeia; aquele que escuta recolhe.
· Com ordem e com tempo encontra-se o segredo de fazer tudo e tudo fazer bem.
· Educai as crianças e não será preciso punir os homens.
· A melhor maneira que o homem dispõe para se aperfeiçoar, é aproximar-se de Deus.
· A Evolução é a Lei da Vida, o Número é a Lei do Universo, a Unidade é a Lei de Deus.
· Ajuda teus semelhantes a levantar a carga, mas não a carregues.

Jogo da Memória

Números: quadrados perfeitos.

Objetivos: trabalha atenção, memória, concentração, estratégia, planejamento, antecipação, aceitação de regras e limites.
Material: 60 peças, sendo 30 com operações matemáticas e 30 com as respectivas respostas.
Número de jogadores: de 2 a 4.
Regras: Embaralhe as peças e espalhe na mesa todas viradas para baixo, num arranjo feito em colunas para facilitar a memorização. Cada jogador deverá levantar duas peças, olhá-las e recolocá-las no lugar, assim é feito até que alguém consiga levantar um par, e então este jogador retira as peças do jogo e as mantém em seu poder; quando um jogador acerta um par tem o direito a mais uma jogada. O jogo termina quando são retiradas da mesa todas as peças, conta-se então o número de peças de cada participante. Vence o jogo quem conseguir o maior número de peças. Variação para contagem dos pontos: a soma dos resultados obtidos.

 

 

Fotos: 5ª A – 2011

Hora de Vencer - André e Felipe - Oficial HD

Festival de Música 2011.

Esse tal de Bhaskara

simulado 2º ano : 1º semestre.

2- Thomas Malthus,clérigo, matemático e economista, influenciou Charles Darwinpor meio de seu livro Ensaio sobre Princípio da População, de 1798, no qual diz que a população humana cresce em PG enquanto as fontes de alimentos crescem em PA, chamada lei de Malthus. O significado dos termos PA e PG que aparecem no texto é:

a) Depois de algum tempo, não haveria alimento para a população, e as pessoas morreriam de fome pela escassez.

b) Depois de algum tempo, haveria muito alimento para a pouca população.

c) É muito lento o crescimento da população em relação aos alimentos.

d) Depois de algum tempo, haveria alimento suficiente para toda população.

e) Depois de algum tempo, haveria alimento para a população, e as pessoas morreriam pela fartura de alimento.

5- Duas pequenas fábricas de calçados, A e B, tem fabricado, respectivamente, 3000 e 1100 pares de sapatos por mês. Se, a partir de janeiro, a fábrica A aumentar sucessivamente a produção em 70 pares e a fábrica B aumentar sucessivamente a produção em 290 pares por mês, a produção da fábrica B superará a produção de A a partir de:

a) Março

b) Maio

c) Julho

d) Setembro

e) Novembro.

http://www.youtube.com/watch?v=g0MqkPEzLUM

Multiplos e divisores.

 

 

Potenciação:

Potenciação

 

Que romântico!!!!

Simulado 1º ano

 

 

Problemas: Função do 1º grau.

Números Inteiros:

Notação científica.

Soma, subtração e multiplicação de Raízes

Atividades sobre solidos geométricos: Cubo, cone, cilindro e pirâmide